Hautbois/Annexe/La physique du hautbois
Le son et l’oreille
[modifier | modifier le wikicode]
L'air est composé de molécules qui sont comme des petites billes qui volent dans tous les sens. Lorsque ces billes frappent une surface, elles exercent une pression dessus. C'est notamment le cas du tympan de notre oreille : lorsque la pression de l’air varie, l'air appuie plus ou moins fort, ce qui déforme le tympan. Le son, c'est lorsque la pression de l’air varie rapidement — plusieurs centaines de fois par seconde — au cours du temps. Ces variations font bouger le tympan, il se met à vibrer, ce qui provoque le phénomène d'audition : notre cerveau analyse les vibrations du tympan et donc détecte les vibrations de l’air, nous entendons le son.
Le nombre de battements par seconde est appelé la fréquence. Elle est exprimée en hertz (abrégé Hz). Les sons audibles ont une fréquence comprise entre 20 Hz (20 battement par seconde) et 20 000 Hz (20 000 battements par seconde) ; plus la fréquence est élevée, plus le son est aigu. La note la de référence correspond à une fréquence de 440 Hz.
La propagation du son dans l'air
[modifier | modifier le wikicode]

Les sons sont des vibrations de l’air.
Imaginons un tuyau. À l'extrémité gauche du tuyau, un piston fait des allers-retours ; il comprime et décomprime l’air du tuyau, alternativement. Dans le tuyau, il se crée des zones de haute densité — les molécules sont resserrées — et de faible densité — les molécules sont écartées. Dans l'image ci-contre, le piston est en rouge et les molécules sont les billes bleues.
On peut voir ça comme la circulation en accordéon sur une autoroute : toutes les voitures vont vers la droite, mais il y a des zones de ralentissement : les voitures ralentissent et se rapprochent les unes des autres, on a une plus forte densité ; et il y a des zones d'accélération : les voitures vont plus vite et s'écartent les unes des autres. Nous remarquons que :
- dans les zones de ralentissement, la vitesse est lente et la densité est forte ;
- dans les zones d'accélération, la vitesse est forte et la densité est faible ;
donc, la densité et la vitesse varient en sens inverse.
La différence est que dans l'air, les molécules ne vont pas toutes en ligne droite, elles vont en diagonale et se cognent contre les parois, et entre elles.
Les sons sont de telles vibrations de l’air : des variations périodiques de densité et de vitesse qui se propagent.
Plutôt que de parler de densité, on préfère parler de pression. La pression, c'est la force avec laquelle l’air pousse sur les surfaces. Plus la densité est importante, plus l'air pousse, plus la pression est grande. Nous dirons donc que le son, les vibrations de l’air, ce sont des variations périodiques de pression et de vitesse de l’air qui se propagent.

Dans un matériau solide, les ondes sont des zones de compression et de détente de la matière qui se propagent, comme illustré dans l'animation ci-contre. À la différence des sons dans l'air, les atomes des solides ne peuvent pas se déplacer sur de longues distances, ils font des allers-retours sur place, mais la situation est similaire.

Si l'air n'est plus contraint par un tuyau, le son se propage de manière concentrique dans toutes les directions.
L'intérieur du hautbois est comme l'intérieur d'un tuyau. On a la création de vibrations qui se propagent linéairement. À la sortie du pavillon du hautbois, le son se propage dans toutes les directions, jusqu'aux oreilles des auditeurs et auditrices.
Le tuyau d'orgue
[modifier | modifier le wikicode]Le tuyau d'orgue permet de comprendre une partie des phénomènes qui surviennent dans le hautbois. À la différence du hautbois :
- il a une perce cylindrique, et non conique ;
- il n'a pas de trou sur sa longueur ;
- nous considérons les tuyaux qui ont un biseau (comme les flûtes à bec), et non une anche (il existe aussi des tuyaux d'orgue à anche, mais le rôle du tuyau est différent) ;
mais comme le hautbois, le tuyau est ouvert à son extrémité (équivalent du pavillon).
À la sortie : la pression de l’air est imposée, c’est la pression atmosphérique. En revanche, la vitesse est libre : l'air peut se diffuser partout, rien ne le contraint. À l'entrée, c'est pareil : la pression de l’air est la pression atmosphérique puisque le biseau est ouvert. Mais la vitesse est inconnue.

Pour voir comment se passe la propagation d'une onde dans un tuyau, voyons comment cela se passe avec de l’eau. Considérons un tuyau d'eau fermé en son milieu par une vanne. Le tuyau est alimenté par la gauche ; la partie droite est vide.
Lorsque l'on ouvre la vanne, l'eau s'écoule dans la partie droite du tuyau. Il y a donc création d'une vague qui se propage vers la droite, vers la sortie. Mais le brusque afflux d'eau vers la droite provoque un déficit à gauche de la vanne : il y a donc une vague en creux qui se propage, elle, vers la gauche.
Lorsque la vague en creux arrive à l'extrémité gauche du tuyau, elle « rebondit ». Et, ce qui est moins intuitif, lorsque la vague « de remplissage », celle qui avance dans la partie droite du tuyau, arrive à la sortie, elle rebondit également : la vague rebondit sur du vide. En effet, l’eau jaillissant hors du tuyau, cela crée un déficit d'eau, une vague en creux qui se propage vers la gauche.
On a donc en permanence un flux d'eau qui va de gauche à droite ; mais à la surface de cette eau, on a des vagues, c'est-à-dire des perturbations sous la forme d'un duo « sommet + creux », qui se propagent dans les deux sens et rebondissent aux extrémités.
Il y a ainsi deux éléments fondamentaux à comprendre :
- une onde est une perturbation ; cette perturbation peut se propager dans toutes les directions, quelle que soit la direction du courant, du vent ; l'onde peut aller à contre-courant ;
- une onde se réfléchit sur une paroi, mais elle se réfléchit aussi sur une ouverture.
Nous avons maintenant deux vagues qui se propagent l'une vers l’autre ; que se passe-t-il à leur rencontre ?
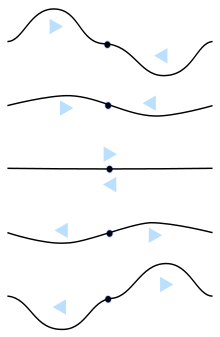
Lorsqu'elles se croisent, on va avoir deux instants :
- l'instant où les deux sommets coïncident, et où les deux creux coïncident : on a une grande vague, le plein s'ajoute au plein, le vide s'ajoute au vide ;
- l'instant où un sommet coïncide avec un creux : le plein remplit le vide, on a une surface plane.

Dans l'image ci-contre, ou voit le croisement de deux trains de vagues : le train de vagues bleues va vers la droite, le train de vagues rouges va vers la gauche, le résultat est le trait noir. On voit que le résultat passe par des états de hauts sommets et grand creux, et des états plats.
La vague résultante, noire, ne se déplace pas : les creux et sommets se forment toujours aux mêmes endroits. On parle d'onde stationnaire.

Maintenant, rappelons-nous que le tuyau d'orgue contient de l’air. Il n'y a donc pas de vague de surface, mais des zones de haute pression et des zones de basse pression. Ces zones se comportent comme des sommets et creux de vague.
Nous avons vu plus haut que la pression de l'air correspondait à une densité : plus la pression est forte, plus l’air est dense. Si nous représentons la pression/densité par une nuance de gris :
- la pression moyenne, c'est-à-dire la pression atmosphérique, est représentée par un gris « moyen » ;
- la pression la plus forte est représentée par le noir ;
- la pression la plus faible est représentée par le blanc ;
alors, l'onde stationnaire dans le tuyau d'orgue est représentée par des variations de gris au cours du temps, comme sur l’animation ci-contre. Nous avons plusieurs ondes stationnaires possibles, nous représentons les trois premiers modes.

La pression est une grandeur qui s'exprime par un nombre, avec une unité (le pascal, Pa, ou plus communément le bar). À un instant t donné, nous pouvons donc représenter la pression en fonction de la position x dans le tuyau, ce qui donne une courbe. Nous représentons ci-contre la correspondance entre la représentation sous forme de niveau de gris et la représentation sous forme de courbe, pour trois instants t, et pour les deux premiers modes.
Les courbes de P(x) forment des vagues qui montent et descendent sur place. Les vagues s'inscrivent donc dans des faisceaux.
Nous avons choisi de représenter les situations à des instants t particuliers. Pour chaque mode i, nous avons une fréquence de vibration ƒi, exprimée en hertz (Hz : battements par seconde) : le mode 1 (mode fondamental) a une fréquence ƒ1, le mode 2 a une fréquence ƒ2… À chaque fréquence correspond une période Ti, exprimée en secondes (s), qui est la durée d'un battement : le mode 1 a une période T1, le mode 2 a une période T2… Avec :
- Ti = 1/ƒi.
Nous choisissons arbitrairement l'instant initial tel que la pression est maximal près de l’entrée du tuyau. Un quart de période après (t = Ti/4), la pression est uniforme, et encore un quart de période après (t = Ti/2), la situation est inversée. Après une période complète (t = Ti), on retrouve la situation initiale.

De la même manière, la vitesse de l’air peut se représenter de deux manières, à chaque instant t :
- par des flèches ;
- par des courbes v(x),
et ces courbes s'inscrivent également dans des faisceaux. Les faisceaux sont étroits lorsque la valeur est constante, large lorsque la valeur varie beaucoup. C'est ce qui figure dans le tableau ci-dessous.
| Paramètre | Tuyau ouvert | Superposition des modes |
|---|---|---|
| Pression | 
|
|
| Vitesse | 
|
Or, chaque mode de vibration a sa fréquence propre ; et la fréquence de vibration correspond à la hauteur de la note (aigu pour les hautes fréquences, grave pour les basses fréquences). Nous voyons donc que :
- le tuyau impose certaines fréquences de vibration de l’air ;
- le mode fondamental correspond à la hauteur de la note ;
- les modes suivants (I, III, …) correspondent aux harmoniques du son, ils déterminent le timbre, la couleur du son.
Comme il impose sa fréquence, le tuyau d'orgue est appelé un « résonnateur ».
La forme en fuseau a deux types de zone :
- les zones de pincement appelés « nœuds » : à ces endroits, la grandeur concernée (pression ou vitesse) ne varie pas ;
- les zones de renflement appelées « ventres » : à ces endroits, la grandeur concernée varie avec une amplitude maximale.
On constate que les nœuds de pression correspondent à des ventres de vitesse, et que les ventres de pression correspondent à des nœuds de vitesse.

Le son réel est une superposition des différents modes ; les fuseaux ne sont donc pas de belles sinusoïdes. Comme dit précédemment, c'est la proportion relative de ces modes, et donc la forme des fuseaux, qui donne la couleur, le timbre de l'instrument.
Ce comportement de type « tuyau d'orgue » décrit bien ce qui se passe dans les flûtes à bec ou traversière, mais pas très bien pour le hautbois, nous le verrons plus bas. Cependant, c'est un exemple permettant de bien comprendre la notion d'onde stationnaire dans un tuyau.
Au final, dans un tuyau d'orgue :
- l'insufflation d'air se fait avec des perturbations, qui provoquent des ondes de pression ;
- les ondes de pression rebondissent aux extrémités du tuyau, contre la paroi du tuyau côté fermé, et contre le « mur d'air » côté ouvert (l’air extérieur étant imperturbable par rapport à ce qui se passe dans le tuyau) ;
- il s'établit très rapidement un régime permanent, dit d'onde stationnaire : selon l'endroit du tuyau, la pression est stable ou bien varie, et de même pour la vitesse ; les zones où la pression est stable (nœuds de pression) sont les zones où la vitesse varie le plus (ventre de vitesse) et à l'inverse, là où la pression varie le plus (ventre de pression), la vitesse est stable (nœud de vitesse) ;
- l'établissement des ventres et des nœuds dépend de la longueur du tuyau ; dans le cas le plus simple, la longueur d'onde λ est la longueur du tuyau ; la fréquence de l'onde dépend de la longueur d'onde λ et de la vitesse du son dans l'air ;
- il existe plusieurs modes de vibration ; le mode fondamental (un seul ventre) détermine la hauteur de la note, les autres modes viennent « colorer » le son et lui donner son timbre.
- Note
- Les lois physiques qui régissent les ondes stationnaires dans un tuyau sont les lois de « l'écoulement compressible à une dimension (1D) », un chapitre de la dynamique des fluides.
Le son et le hautbois
[modifier | modifier le wikicode]Le hautbois, comme tous les instruments de musique, est donc un outil servant à créer des vibrations de l’air.
Lorsque l'on souffle dans l'anche, cela la met en vibration : les lamelles de roseau s'écartent et se rapprochent de manière périodique. Le corps du hautbois est, comme le tuyau d'orgue, un résonnateur. La fréquence de vibration est déterminée par le corps du hautbois et les trous qui sont ouverts.
Par rapport au tuyau d'orgue vu précédemment, il y a donc trois différences majeures : la présence de tour, la perce conique et l’anche à l’entrée.
La présence de trous ouverts
[modifier | modifier le wikicode]Le corps de l'instrument est percé de trous. Si le trou est ouvert, alors à cet endroit-là, la pression est égale à la pression atmosphérique (nœud de pression), et l'air peut entrer et sortir librement (ventre de vitesse). Cela impose donc une forme à l'onde.
Le fait de boucher et déboucher des trous modifie donc la position des ventres et des nœuds, et ainsi la fréquence de l'onde (soit la hauteur de la note), ainsi que les harmoniques (donc sa sonorité).
Dans la description que nous venons de faire, la taille du trou n'intervient pas, en quoi un demi-trou serait différent d'un trou totalement ouvert ? Nous voyons donc que la réalité est plus complexe que cela[1].
La forme et le taille des perçages affectent le son. Dans le cas du hautbois[2] :
- les trous ont un petit diamètre, l'onde se propage donc jusqu'au pavillon (si les trous étaient plus larges, l’air s'échapperait plus par les trous et l'onde ne s'étendrait pas aussi loin) :
- les trous sont chambrés : le diamètre augmente en s'étageant lorsque l'on va vers l’extérieur, pour « laisser le son s'échapper » et éviter d'avoir un son étouffé ;
- les trous présentent un dégagement à l'intérieur : le diamètre côté intérieur est également plus important qu'au centre du perçage, ce qui permet d'avoir un son plus brillant.

L’anche à l’entrée
[modifier | modifier le wikicode]Alors que pour le tuyau d'orguen l'ouverture biseautée impose la pression atmosphérique, ici, l’anche a un rôle complexe[3] ; quand le ou la hautboïste ne joue pas trop fort, on peut estimer que l'instrumentiste impose un débit d'air à peu près constant, la pression étant variable. Nous ne sommes donc plus dans la situation d'un tuyau ouvert aux deux extrémités, mais d'un tuyau semi-ouvert, à l'image d'une flûte de pan (ou d'un tuyau d'orgue bouché, un gedackt), mais à l'envers :
- pour la flûte de pan (tuyau semi-ouvert), l'ouverture libre est côté bouche ;
- pour le hautbois, la clarinette, le basson ou le saxophone, l'ouverture est le pavillon, le côté bouche est le côté fermé.
Pour décrire la situation de manière plus précise :
- lorsque l'instrumentiste souffle, l'air accélère pour passer dans la petite ouverture de l'anche ;
- cette accélération de l’air provoque une dépression dans l'anche (par effet Venturi) ; cette dépression a tendance à refermer l'anche ;
- le rapprochement des lamelles de roseau crée une surpression qui suit la dépression, comme quand on claque des mains ;
- on a ainsi une onde de pression (une dépression suivie d'une surpression) qui voyage dans le corps du hautbois et se réfléchit sur les zones ouvertes (trou ouvert ou bien pavillon) et revient vers l'anche ;
- le retour de la surpression vient rouvrir l'anche.
Le processus se poursuit, et, le corps du hautbois jouant son rôle de résonateur, l'anche vibre au rythme imposé par le tuyau.
La situation devient plus complexe à partir d'une certaine pression où l’anche devient « battante » (elle se ferme complètement de manière cyclique).
|
L'effet Venturi Une quantité donnée d'air « emporte » une certaine quantité d'énergie. Cette énergie est de trois ordres :
Si l'on néglige les frottements, l'énergie totale est constante, elle ne varie pas :
Si l'on divise tout par la masse, on obtient :
où ρ est la masse volumique de l'air (en kg/m³). Comme la valeur de e est constante, si un élément augmente, l'autre diminue nécessairement. Donc, lorsque la vitesse augmente, la pression diminue
c'est l'effet Venturi. |
La forme conique
[modifier | modifier le wikicode]Ce que nous avons décrit plus haut est valable pour les instruments à perce cylindrique, comme les clarinettes ou les bassons. La forme conique de la perce du hautbois rend les choses plus complexes.
En raison de la perce conique[4], la réflexion côté embouchure se fait comme si la paroi était le sommet du cône, à l'extérieur de l’instrument. De fait, la longueur d'onde λ0 de la fondamentale est le double de la longueur L du cône, λ0 = 2L[5]. La longueur du cône est substantiellement différente de la longueur réelle de l'instrument : le demi-angle au sommet étant faible, environ 0,7°, la partie tronquée s'étend au-delà de l’extrémité de l’anche.
Si le cône était fermé jusqu'à son sommet, alors le comportement serait similaire à celui d'un tuyau ouvert. Mais cette situation n’est pas possible, il faut nécessairement tronquer le cône pour pouvoir introduire l'air à travers un trou de diamètre suffisant. Les harmoniques du hautbois sont donc entre celles d'un tuyau semi-ouvert et d'un tuyau ouvert des deux côtés[6].
Voir aussi
[modifier | modifier le wikicode]Notes et références
[modifier | modifier le wikicode]- ↑ (en) Jean-Baptiste Doc, Christophe Langrenne et Alexandre Garcia, « Influence of the Side Holes Geometry in the Resonance and Acoustic Radiation of Wind Instruments », Forum Acusticum 2020, 25 mai 2021 [lien DOI].
- ↑ (en) « How the Oboe is Made: The sound is adjusted based on the shape of the tone hole? », sur Yamaha (consulté le 1er février 2024).
- ↑ Dalmont et Kergomard 2008, p. 61, encadré L'anche, une porte qui bat.
- ↑ Dalmont et Kergomard 2008, p. 62, figure 4 Dans un instrument à anche conique.
- ↑ Wolfe 2018.
- ↑ (en) Michael J. Ruiz, « Hearing the transformation of conical to closed-pipe resonances », Physics Education, 30 mars 2017 [lien DOI].
Bibliographie et liens
[modifier | modifier le wikicode]- Jean-Pierre Dalmont et Jean Kergomard, « Le rythme des anches », Pour la science, no 373, novembre 2008, p. 58-63
- L. F. Almeida et coll., « Physical model of an oboe: comparison with experiments », sur CNRS, (consulté le 20 décembre 2023)
- [Wolfe 2018] (en) Joe Wolfe, « Double reed acoustics: oboe, bassoon and others », sur Université de Nouvelle-Galles du Sud (Australie), 2018 (consulté le 6 mars 2024)
- (en) Jan Bouterse, « Acoustical aspects of the baroque oboe », The Fellowship of Makers and Researchers of Historical Instruments (FoMRHI), no 143, septembre 2018 [texte intégral (page consultée le 2024-03-06)]
- (en) Jan Bouterse, « Tuning the baroque oboe », The Fellowship of Makers and Researchers of Historical Instruments (FoMRHI), no 143, septembre 2018 [texte intégral (page consultée le 2024-03-06)]








