Résistance et impédance/Loi d'Ohm

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Dipôle résistant, loi d'Ohm

Résistance

En électricité, le terme résistance désigne différentes choses, qui restent toutefois liées :

• une propriété physique : l'aptitude d’un matériau conducteur à ralentir le passage du courant électrique ;
• un dipôle électrique qui est utilisé soit pour réduire l'intensité du courant (rhéostat), soit pour obtenir en un point un potentiel déterminé (diviseur de tension - il faut alors au moins deux résistances) ou encore produire de l'énergie thermique ;
• un modèle mathématique qui respecte idéalement la loi d'Ohm, baptisé conducteur ohmique ou résistance idéale et qui permet de modéliser les dipôles réels ;
• un composant électronique conçu pour approcher de manière très satisfaisante la loi d'Ohm dans une large plage d’utilisation.

Dipôle passif

Une résistance est toujours un dipôle passif.

Définition

On appelle dipôle passif, un dipôle récepteur dans lequel toute l'énergie électrique est dissipée en énergie thermique.

• 
  Résistor
• 
  Ampoule à incandescence

Début de l'exemple

Exemple

Une lampe à incandescence, un radiateur électrique sont des dipôles passifs.

Fin de l'exemple

• Contre-Exemple : Un moteur électrique n'en est pas un.

Loi d'Ohm

Définition

Un dipôle récepteur passif respecte la loi d'Ohm si la tension à ses bornes est rigoureusement proportionnelle à l'intensité du courant qui le traverse.

La loi d'Ohm s'applique assez bien aux conducteurs métalliques thermostatés (c'est-à-dire dont la température est maintenue constante)

Début d’un principe

Principe

Tant que la température du dipôle résistant est constante, la tension aux bornes d’un conducteur métallique est proportionnelle au courant ; la résistance du dipôle est constante.

Fin du principe

Caractéristique tension courant d'une résistance

Définition

On appelle caractéristique tension-courant d’un dipôle, la courbe $U=f(I)$ représentant la tension aux bornes du dipôle en fonction du courant qui la traverse.

De même, on peut définir la caractéristique courant-tension.

À noter que, ici encore, il s'agit d’une modélisation qui comporte des limites. Pour certains dipôles dont les inductances ou les condensateurs qui seront mentionnés dans ce cours, la courbe obtenue dépend de l'histoire du dipôle. Par exemple, on a pas forcément la même courbe quand on réalise la mesure avec U croissant ou avec U décroissant. La caractéristique, elle aussi, a un domaine de validité.

Définition

On appelle résistance idéale ou conducteur ohmique, un dipôle dont la caractéristique est une droite passant par l'origine.

Analyse physique de la caractéristique d’une résistance réelle

Jusqu'à une certaine valeur du courant, la caractéristique d’une résistance utilisée en électronique est pratiquement une droite qui passe par l'origine des coordonnées
Donc, tant que le courant est inférieur à cette valeur, la caractéristique $U=f(I)$ est de la forme linéaire $y=ax$ soit, ici, $U=aI$ dans laquelle $a$ est une constante.
Ensuite, la caractéristique s'incurve. La caractéristique montre que la tension n'est plus proportionnelle au courant.

Résistance électrique

Loi d'Ohm

Définition

Le rapport ${U \over I}$, de la tension aux bornes du dipôle au courant qui le traverse, est appelé la résistance électrique $R$ du dipôle, au courant $I$.

La relation $R={U \over I}$ définit la résistance.
Son unité s'exprime en volts par ampère ; ce sont aussi des ohms : $\Omega$
À noter que la résistance électrique correspond au coefficient directeur de la caractéristique du dipôle résistance exprimé en V/A.

C'était pour éviter la confusion entre la résistance (dipôle) et la résistance (grandeur électrique définissant une propriété du dipôle) que le terme de « résistor » avait été introduit dans les programmes de l’enseignement français.

L'application de la loi d'Ohm à la mesure de la résistance est une méthode simple, c’est la méthode volt-ampèremétrique qui peut être extrêmement précise si l’on tient compte des perturbations engendrées par les appareils de mesure.

Exercices

Faites ces exercices : Loi d'Ohm 1.

Calcul de la résistance

La méthode volt-ampèremétrique permet de mesurer la résistance d’un conducteur. Mais pour les conducteurs simples et homogènes qui sont définis par des dimensions et une nature de matière. Il est possible, en fonction de ces différents paramètres, de déterminer la valeur de leur résistance.

Influence de la longueur

Début d’un principe

Principe

On alimente, en mesurant sa tension et son courant, un morceau de conducteur dont on peut en faire varier la longueur sans modifier ses autres paramètres (section, température) et on remplit un tableau de mesure.

Fin du principe

Longueur	Ampèremètre	Voltmètre	Résistance
0,5 m	100 mA	0,106 V	1,06 $\Omega$
0,75 m	100 mA	0,161 V	1,61 $\Omega$
1 m	100 mA	0,210 V	2,10 $\Omega$

Aux incertitudes près, on constate que la résistance évolue de façon proportionnelle avec la longueur de fil utilisée.

Propriété

La résistance d’un fil est proportionnelle à la longueur.

Influence de la section

Début d’un principe

Principe

On alimente, en mesurant sa tension et son courant, différents conducteurs de sections différentes, mais sans modifier ses autres paramètres (nature du conducteur, température et longueur) et on remplit un tableau de mesure.

Fin du principe

Section	Ampèremètre	Voltmètre	Résistance
0,5 mm2	100 mA	0,637 V	6,37 $\Omega$
0,75 mm2	100 mA	0,424 V	4,24 $\Omega$
1 mm2	100 mA	0,312 V	3,12 $\Omega$
1,5 mm2	100 mA	0,210 V	2,10 $\Omega$

À première vue, on ne peut pas définir une relation directe entre la section et la résistance.
En observant attentivement le tableau, on constate qu'en doublant la section (de 0,5 mm² à 1 mm²), la résistance est presque de moitié (6,37 pour 3,12). On observe le même rapport en comparant 0,5 mm² et 1,5 mm² (rapport de 3) et en comparant 0,75 mm² et 1,5 mm² (rapport de 2).

Propriété

La résistance d’un fil est inversement proportionnelle à la section du fil.

Influence de la nature du fil

À partir des deux constatations précédentes, en posant $l$ la longueur d’un conducteur et $s$ sa section, on peut écrire que :
$R=k{\frac {l}{s}}$

Il reste à définir le coefficient $k$. Pour cela, on va prendre des conducteurs de matériaux différents et effectuer les mêmes types de mesure que précédemment.

Nature du conducteur	$k$
Cuivre	$23\times 10^{-9}$
Aluminium	$32\times 10^{-9}$
Fer	$117\times 10^{-9}$

Propriété

La nature du matériau modifie le paramètre $k$.

Ce paramètre, lié seulement à la nature du matériau est appelé résistivité du matériau.

Définition

On appelle résistivité électrique $\rho$ d’un matériau, le coefficient qui entre dans le calcul de sa résistance électrique à partir de ses dimensions physiques.

Son unité est définie par :
$[R]=[\rho ]{[l] \over [s]}$
donc $[\rho ]={{[R][s]} \over [l]}$
$[\rho ]={{\Omega \times m^{2}} \over m}\equiv \Omega m$

Définition

L'unité de la résistivité électrique est l'ohm.mètre carré par mètre (Ωm²/m) ou plus simplement l'ohm.mètre (Ωm).

Pour connaître la valeur de résistivité de certains matériaux, consulter l’article sur Wikipédia.

Influence de la température

Pour déterminer l'influence de la température sur la résistivité d’un matériau, il faut faire le calcul suivant : R(θ) = R0*(1 + a*θ)

a est la conductivité du matériau en question ; θ veut dire « X °C » ; R(θ) est la résistance à X °C ; R0 est la résistance initiale.

Exercices

Faites ces exercices : Loi d'Ohm 2.

Mesure de la résistance électrique

Avec un ohmmètre

Pour mesurer la valeur d’une résistance avec un ohmmètre, il faut que cette résistance soit déconnectée de son montage (sinon on mesure la résistance du montage).

On connecte la résistance à mesurer aux deux bornes de l'appareil de mesure (l'ohmmètre) et on lit directement la valeur indiquée. En général, ces appareils utilisent la méthode volt-ampèremétrique (ci-dessous) et la loi d'Ohm : ils injectent un courant constant et connu à travers le dipôle et mesurent la tension qui est convertie en valeur de résistance.

Avec la méthode volt-ampèremétrique

Utilisant la loi d'Ohm ($R={\frac {U}{I}}$), on fait circuler un courant dans l'élément dont on veut connaitre la résistance et on mesure la tension. Il faut donc deux appareils de mesure (un voltmètre et un ampèremètre).

L'avantage de ce montage est que l’on peut mesurer une résistance « à chaud », c'est-à-dire dans les conditions de températures proches de celle de son utilisation normale.

Il faut faire attention à ce que les résistances internes des appareils de mesure ne viennent perturber les mesures. pour cela il existe deux types de montage :

• le montage aval ;
• le montage amont.

Montage aval

L'ampèremètre se place avant le voltmètre. La valeur de la tension est exacte mais on fait donc une erreur sur le courant mesuré car l'ampèremètre prend en compte le courant qui traverse la résistance interne du voltmètre, en plus de celle du système mesuré. On mesure donc en toute rigueur la résistance équivalente du dipôle en parallèle avec le voltmètre. Cette méthode est intéressante pour les dipôles dont la résistance est faible par rapport à celle du voltmètre, généralement de l’ordre du MΩ. Si elles sont proches, la connaissance de la résistance interne du voltmètre permet de calculer la résistance du dipôle.

Montage amont

Le voltmètre mesure la tension au borne de l’ensemble « ampèremètre - dipôle ». La valeur du courant est exacte mais on fait une erreur sur la tension. On mesure donc en toute rigueur la résistance équivalente du dipôle en série avec l'ampèremètre. Cette méthode est intéressante pour les dipôles dont la résistance est forte par rapport à celle de l'ampèremètre (rarement supérieure au kΩ). Comme précédemment, si besoin, la connaissance de la résistance interne de l'ampèremètre permet de calculer la résistance exacte du dipôle.

À l'aide d'un pont de Wheatstone

Pont de Wheatstone

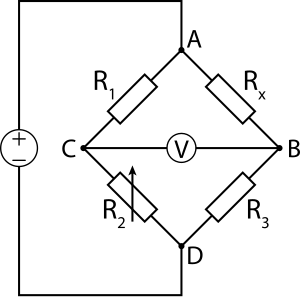
Le pont de Wheatstone est un système de mesure de résistance par comparaison.

Il s'agit de deux branches potentiométriques que l’on « équilibre ».

• Le potentiel du point B est défini par les valeurs des résistances $R_{3}$ et $R_{x}$ (relation du diviseur de tension).
• Le potentiel du point C est défini par celles des résistances $R_{2}$ et $R_{1}$. $R_{2}$ étant variable, on l’ajuste pour que les deux potentiels soient égaux.

Si l’on prend l'exemple ci-contre :

• soit $R_{1}$ et $R_{3}$ sont des résistances parfaitement connues ;
• soit $R_{x}$ est la résistance que l’on cherche à mesurer.

Il suffit de modifier $R_{2}$ afin que le voltmètre affiche simplement 0.

Alors on a l'égalité suivante :

$R_{x}={\frac {R_{1}\times R_{3}}{R_{2}}}$

Début d'une démonstration

Démonstration

Si aucun courant ne circule dans le voltmètre, ce qui ne peut être vrai que si ce dernier affiche 0, et que la tension d'alimentation du montage vaut U :

La tension du point C vaut : $U_{C}=U\times {\frac {R_{2}}{R_{1}+R_{2}}}$

La tension du point B vaut : $U_{B}=U\times {\frac {R_{3}}{R_{x}+R_{3}}}$

Si le voltmètre indique 0, alors $U_{B}=U_{C}$ donc $U\times {\frac {R_{2}}{R_{1}+R_{2}}}=U\times {\frac {R_{3}}{R_{x}+R_{3}}}$

d'où ${\frac {R_{2}}{R_{1}+R_{2}}}={\frac {R_{3}}{R_{x}+R_{3}}}$

donc $R_{2}\times R_{x}+R_{2}\times R_{3}=R_{1}\times R_{3}+R_{2}\times R_{3}$

soit $R_{2}\times R_{x}=R_{1}\times R_{3}$

et enfin $R_{x}={\frac {R_{1}\times R_{3}}{R_{2}}}$

Fin de la démonstration

L'avantage du pont de Wheatstone est que le résultat est indépendant de la valeur de la tension de l'alimentation (on peut aussi utiliser une tension alternative) et indépendante de la résistance interne du voltmètre. On peut même remplacer le voltmètre par un ampèremètre quand le pont est presque équilibré afin d'avoir une très grande sensibilité. L'inconvénient est sa complexité. À noter qu'il existe des ponts de mesure automatiques.