Statistique à deux variables/Séries de données statistiques quantitatives à deux variables
Série statistiques à deux variables
[modifier | modifier le wikicode]et désignent deux variables statistiques quantitatives observées sur individus d'une même population.
Pour , et désignent les mesures relevées pour et .
Les couples forment une série statistique à deux variables.
Remarque : Nous pouvons étudier séparément chacune des séries X et Y comme des séries statistiques à une variable et calculer leurs moyennes, médiane, écart-type, etc. Voir Statistique à une variable. Dans la présente leçon, ce sont les relations entre X et Y qui nous intéressent.
Nuage de points
[modifier | modifier le wikicode]Dans un repère orthogonal, on peut représenter l’ensemble des points .
Ils forment le nuage de points de la série (X;Y)
Notation
[modifier | modifier le wikicode]Pour simplifier l'exposé des formules, nous utiliserons la notation
pour signifier la somme sur toutes les valeurs prises par .
Par exemple :
Point moyen
[modifier | modifier le wikicode]
Ajustement
[modifier | modifier le wikicode]Lorsque les deux variables et sont liées l'une à l'autre, on peut s'attendre à ce que le nuage de points présente une forme particulière.
Effectuer un ajustement de en d'un nuage de points consiste à trouver
une fonction telle que la courbe passe "le plus près possible" des points du nuage.
Remarque : la courbe peut être une droite ou une parabole.
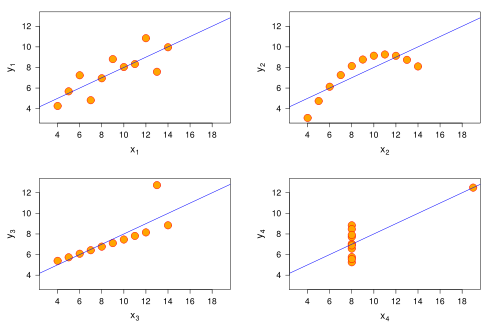
ou bien il peut ne pas y avoir de courbe visible :

Parfois, une courbe est suggérée mais ne correspond pas parfaitement au nuage :

Méthodes sommaires d'ajustement affine
[modifier | modifier le wikicode]Deux méthodes peuvent être proposées pour une approche rapide de la notion d'ajustement affine.
- La méthode empirique : l'opérateur choisit parmi les droites passant par le point moyen G celle qui lui semble épouser au mieux l'allure du nuage. Peu rigoureuse, cette méthode est très subjective.
- La méthode de Mayer : l'opérateur partage le nuage de points en deux parties de même effectif, éventuellement à une unité près, puis détermine les points moyens et de chaque sous-nuage. La droite retenue est alors dont on démontre qu'elle passe nécessairement par G. Malgré son apparence plus mathématique, cette méthode - enseignée dans certaines classes pour sa facilité d'accès - est d'une validité aléatoire.

























