En raison de limitations techniques, la typographie souhaitable du titre, «
Exercice : La RésistanceRésistance et impédance/Exercices/Résistance », n'a pu être restituée correctement ci-dessus.
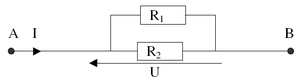
R
1
=
100
Ω
{\displaystyle R_{1}=100\Omega }
R
2
=
50
Ω
{\displaystyle R_{2}=50\Omega }
Solution
R
e
q
=
R
1
+
R
2
{\displaystyle R_{eq}=R_{1}+R_{2}}
R
e
q
=
100
+
50
{\displaystyle R_{eq}=100+50}
R
e
q
=
150
Ω
{\displaystyle R_{eq}=150\Omega }
R
1
=
100
Ω
{\displaystyle R_{1}=100\Omega }
R
2
=
50
Ω
{\displaystyle R_{2}=50\Omega }
Solution
R
e
q
=
1
1
R
1
+
1
R
2
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}}
R
e
q
=
1
1
100
+
1
50
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{100}}+{\frac {1}{50}}}}}
R
e
q
=
1
1
100
+
2
100
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{100}}+{\frac {2}{100}}}}}
R
e
q
=
1
3
100
{\displaystyle R_{eq}={\frac {1}{\frac {3}{100}}}}
R
e
q
=
100
3
{\displaystyle R_{eq}={\frac {100}{3}}}
R
e
q
=
33
,
3
Ω
{\displaystyle R_{eq}=33,3\Omega }
R
1
=
100
Ω
{\displaystyle R_{1}=100\Omega }
R
2
=
50
Ω
{\displaystyle R_{2}=50\Omega }
R
3
=
200
Ω
{\displaystyle R_{3}=200\Omega }
Solution
R
e
q
1
=
1
1
R
1
+
1
R
2
{\displaystyle R_{eq_{1}}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}}
R
e
q
=
R
e
q
1
+
R
3
{\displaystyle R_{eq}=R_{eq_{1}}+R_{3}}
R
e
q
=
1
1
R
1
+
1
R
2
+
R
3
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}+R_{3}}
R
e
q
=
1
1
100
+
1
50
+
200
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{100}}+{\frac {1}{50}}}}+200}
R
e
q
=
1
1
100
+
2
100
+
200
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{100}}+{\frac {2}{100}}}}+200}
R
e
q
=
1
3
100
+
200
{\displaystyle R_{eq}={\frac {1}{\frac {3}{100}}}+200}
R
e
q
=
100
3
+
200
{\displaystyle R_{eq}={\frac {100}{3}}+200}
R
e
q
=
33
,
3
+
200
{\displaystyle R_{eq}=33,3+200}
R
e
q
=
233
,
3
Ω
{\displaystyle R_{eq}=233,3\Omega }
R
1
=
100
Ω
{\displaystyle R_{1}=100\Omega }
R
2
=
50
Ω
{\displaystyle R_{2}=50\Omega }
R
3
=
200
Ω
{\displaystyle R_{3}=200\Omega }
R
4
=
75
Ω
{\displaystyle R_{4}=75\Omega }
Solution
R
e
q
1
=
1
1
R
1
+
1
R
2
{\displaystyle R_{eq_{1}}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}}
R
e
q
=
R
e
q
1
+
R
3
+
R
4
{\displaystyle R_{eq}=R_{eq_{1}}+R_{3}+R_{4}}
R
e
q
=
1
1
R
1
+
1
R
2
+
R
3
+
R
4
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}+R_{3}+R_{4}}
R
e
q
=
1
1
100
+
1
50
+
200
+
75
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{100}}+{\frac {1}{50}}}}+200+75}
R
e
q
=
1
1
100
+
2
100
+
275
{\displaystyle R_{eq}={\frac {1}{{\frac {1}{100}}+{\frac {2}{100}}}}+275}
R
e
q
=
1
3
100
+
275
{\displaystyle R_{eq}={\frac {1}{\frac {3}{100}}}+275}
R
e
q
=
100
3
+
275
{\displaystyle R_{eq}={\frac {100}{3}}+275}
R
e
q
=
33
,
3
+
275
{\displaystyle R_{eq}=33,3+275}
R
e
q
=
308
Ω
{\displaystyle R_{eq}=308\Omega }
R
1
=
100
Ω
{\displaystyle R_{1}=100\Omega }
R
2
=
50
Ω
{\displaystyle R_{2}=50\Omega }
R
3
=
200
Ω
{\displaystyle R_{3}=200\Omega }
R
4
=
75
Ω
{\displaystyle R_{4}=75\Omega }
R
5
=
400
Ω
{\displaystyle R_{5}=400\Omega }
R
6
=
25
Ω
{\displaystyle R_{6}=25\Omega }
R
1
=
100
Ω
{\displaystyle R_{1}=100\Omega }
R
2
=
50
Ω
{\displaystyle R_{2}=50\Omega }
R
3
=
200
Ω
{\displaystyle R_{3}=200\Omega }
R
4
=
75
Ω
{\displaystyle R_{4}=75\Omega }
R
10
=
30
Ω
{\displaystyle R_{10}=30\Omega }
R
11
=
25
Ω
{\displaystyle R_{11}=25\Omega }
R
12
=
80
Ω
{\displaystyle R_{12}=80\Omega }
R
13
=
66
Ω
{\displaystyle R_{13}=66\Omega }
R
20
=
33
Ω
{\displaystyle R_{20}=33\Omega }
R
21
=
125
Ω
{\displaystyle R_{21}=125\Omega }
R
22
=
17
Ω
{\displaystyle R_{22}=17\Omega }
R
23
=
50
Ω
{\displaystyle R_{23}=50\Omega }
Nous disposons d'un système de chauffage qui, grâce à un système de commutateur permet d’avoir 3 puissances de chauffe.
En manoeuvrant le contacteur, on commute 5 interrupteurs qui s'ouvre ou se ferme suivant le tableau ci-dessous
Couplage
Position des contacts (O=Ouvert ou F=Fermé)
K1
K2
K3
K4
K5
1er couplage
F
F
O
O
O
2e couplage
F
O
O
F
F
3e couplage
F
F
F
F
O
Le montage électrique du système est le suivant :
On donne les informations suivantes :
U = 230 V
R
1
{\displaystyle R_{1}}
Ω et
R
2
{\displaystyle R_{2}}
Ω Dessiner le schéma équivalent au montage en remplaçant un contact fermé par un conducteur et un contact ouvert par rien
Pour ce couplage, déterminer la résistance équivalente à ce montage :
Solution
R =
R
1
{\displaystyle R_{1}}
Ω
Calculer le courant I absorbé par le montage :
Solution
Formule
U = RI
U
R
{\displaystyle {\frac {U}{R}}}
Application numérique
I =
230
6
{\displaystyle {\frac {230}{6}}}
Résultat
I = 38,3 A
Calculer la puissance dissipée par le montage :
Solution
Formule
P =
U
2
R
{\displaystyle {\frac {U^{2}}{R}}}
Application numérique
P =
230
2
6
{\displaystyle {\frac {230^{2}}{6}}}
8
,
82.10
3
{\displaystyle 8,82.10^{3}}
230
×
38
,
3
{\displaystyle 230\times 38,3}
8
,
81.10
3
{\displaystyle 8,81.10^{3}}
Résultat
P = 8,82 kW
Dessiner le schéma équivalent au montage en remplaçant un contact fermée par un conducteur et un contact ouvert par rien
Pour ce couplage, Calculer la résistance équivalente à ce montage :
Solution
Formule
R =
R
1
+
R
2
{\displaystyle R_{1}+R_{2}}
Application numérique R = 6 + 12
Résultat R = 18 Ω
Calculer le courant I absorbé par le montage :
Solution
Formule
U = RI
U
R
{\displaystyle {\frac {U}{R}}}
Application numérique
I =
230
18
{\displaystyle {\frac {230}{18}}}
Résultat
I = 12,8 A
Calculer la puissance dissipée par le montage :
Solution
Formule
P =
U
2
R
{\displaystyle {\frac {U^{2}}{R}}}
Application numérique
P =
230
2
18
{\displaystyle {\frac {230^{2}}{18}}}
2
,
94.10
3
{\displaystyle 2,94.10^{3}}
230
×
12
,
8
{\displaystyle 230\times 12,8}
2
,
94.10
3
{\displaystyle 2,94.10^{3}}
Résultat
P = 2,94 kW
Dessiner le schéma équivalent au montage en remplaçant un contact fermé par un conducteur et un contact ouvert par rien
Pour ce couplage, Calculerla résistance équivalente à ce montage :
Solution
Formule
R =
R
1
×
R
2
R
1
+
R
2
{\displaystyle {\frac {R_{1}\times R_{2}}{R_{1}+R_{2}}}}
1
R
=
1
R
1
+
1
R
2
{\displaystyle {\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}
Application numérique R =
6
×
12
6
+
12
{\displaystyle {\frac {6\times 12}{6+12}}}
1
R
=
1
6
+
1
12
{\displaystyle {\frac {1}{R}}={\frac {1}{6}}+{\frac {1}{12}}}
Résultat R = 4 Ω
Calculer le courant I absorbé par le montage :
Solution
Formule
U = RI
U
R
{\displaystyle {\frac {U}{R}}}
Application numérique
I =
230
4
{\displaystyle {\frac {230}{4}}}
Résultat
I = 57,5 A
Calculer la puissance dissipée par le montage :
Solution
Formule
P =
U
2
R
{\displaystyle {\frac {U^{2}}{R}}}
Application numérique
P =
230
2
4
{\displaystyle {\frac {230^{2}}{4}}}
13
,
2.10
3
{\displaystyle 13,2.10^{3}}
230
×
57
,
5
{\displaystyle 230\times 57,5}
13
,
2.10
3
{\displaystyle 13,2.10^{3}}
Résultat
P = 13,2 kW
On se retrouve de nouveau avec un système de chauffage qui permet de coupler 3 résistances de façon différente afin d'obtenir 4 puissances de chauffe.
Chacune des résistances est identique et sa caractéristique est : 230 V kW
On se retrouve donc avec les 4 schémas électriques suivants :
Calculer la valeur d'une résistance :
Solution
Formule
P =
U
2
R
{\displaystyle {\frac {U^{2}}{R}}}
U
2
P
{\displaystyle {\frac {U^{2}}{P}}}
Application numérique
R =
230
2
1000
{\displaystyle {\frac {230^{2}}{1000}}}
Résultat
R = 52,9 Ω
Dans toute la suite de l'exercice, R = 53 Ω Calculer la résistance équivalent
R
e
q
1
{\displaystyle R_{eq_{1}}}
Solution
Formule
R
e
q
1
{\displaystyle R_{eq_{1}}}
Application numérique
R
e
q
1
=
3
×
53
{\displaystyle R_{eq_{1}}=3\times 53}
Résultat
R
e
q
1
{\displaystyle R_{eq_{1}}}
Ω
Calculer la résistance équivalent
R
e
q
2
{\displaystyle R_{eq_{2}}}
Solution
Formule
1
R
e
q
2
=
1
R
+
1
R
+
1
R
{\displaystyle {\frac {1}{R_{eq_{2}}}}={\frac {1}{R}}+{\frac {1}{R}}+{\frac {1}{R}}}
1
R
e
q
2
=
3
R
{\displaystyle {\frac {1}{R_{eq_{2}}}}={\frac {3}{R}}}
R
e
q
2
=
R
3
{\displaystyle R_{eq_{2}}={\frac {R}{3}}}
Application numérique
R
e
q
2
=
53
3
{\displaystyle R_{eq_{2}}={\frac {53}{3}}}
Résultat
R
e
q
2
{\displaystyle R_{eq_{2}}}
Ω
Calculer la résistance équivalent
R
e
q
3
{\displaystyle R_{eq_{3}}}
Solution
Formule
R
e
q
3
=
R
+
R
×
R
R
+
R
=
R
+
R
2
{\displaystyle R_{eq3}=R+{\frac {R\times R}{R+R}}=R+{\frac {R}{2}}}
R
e
q
3
=
53
+
53
2
{\displaystyle R_{eq3}=53+{\frac {53}{2}}}
Résultat
R
e
q
3
{\displaystyle R_{eq_{3}}}
Ω
Calculer la résistance équivalent
R
e
q
4
{\displaystyle R_{eq_{4}}}
Solution
Formule
R
e
q
4
=
(
R
+
R
)
×
R
(
R
+
R
)
+
R
{\displaystyle R_{eq4}={\frac {(R+R)\times R}{(R+R)+R}}}
Application numérique
R
e
q
4
=
(
53
+
53
)
×
53
(
53
+
53
)
+
53
{\displaystyle R_{eq4}={\frac {\left(53+53\right)\times 53}{(53+53)+53}}}
Résultat
R
e
q
4
{\displaystyle R_{eq4}}
Ω
Pour quelle association des résistances la puissance dissipée est-elle maximale, calculer la valeur de cette puissance.
Solution
Formule
P
=
U
2
R
{\displaystyle P={\frac {U^{2}}{R}}}
Donc la puissance sera maximale, lorsque la résistance sera minimale, donc elle l'est pour le montage de la figure 2
Application numérique
P
m
a
x
=
U
2
R
e
q
2
=
230
2
17
,
7
=
2
,
99.10
3
{\displaystyle P_{max}={\frac {U^{2}}{R_{eq2}}}={\frac {230^{2}}{17,7}}=2,99.10^{3}}
Résultat
P
m
a
x
{\displaystyle P_{max}}
kW
Pour quelle association des résistances la puissance dissipée est-elle minimale, calculer la valeur de cette puissance.
Solution
Formule
P
=
U
2
R
{\displaystyle P={\frac {U^{2}}{R}}}
Donc la puissance sera minimale, lorsque la résistance sera maximale, donc elle l'est pour le montage de la figure 1
Application numérique
P
m
i
n
=
U
2
R
e
q
1
=
230
2
159
{\displaystyle P_{min}={\frac {U^{2}}{R_{eq1}}}={\frac {230^{2}}{159}}}
Résultat
P
m
i
n
{\displaystyle P_{min}}
W
On se retrouve avec un montage électronique dessiné comme ci-dessous, avec pour chacune des résistances les valeurs suivantes :
R1 = 150 Ω
R2 = 20 Ω
R3 = 600 Ω
R4 = 120 Ω
R5 = 100 Ω
R6 = 80 Ω On sait que le courant dans une des résistances est :
Calculer la tension d'alimentation U
Solution
Formule
U = R I
Application numérique
U = 1,5 × 150 = 225
Résultat
U = 225 V
Calculer la résistance équivalente (R) du montage.
Solution
Formule
Application numérique
Résultat R = 75 Ω
Calculer le courant (I) qu'absorbe le circuit électronique :
Solution
Formule
U = RI
U
R
{\displaystyle {\frac {U}{R}}}
Application numérique
I =
225
75
{\displaystyle {\frac {225}{75}}}
Résultat
I = 3 A