Lentilles en optique géométrique/Lentilles minces sphériques
Les lentilles sphériques sont souvent formées d’un morceau de verre taillé comportant deux faces étant soit planes soit sphériques. Selon qu’il y ait une ou deux surfaces sphériques, elles sont appelées plan-convexe, plan-concave, biconvexe, biconcave…
Chaque face étant une portion de sphère, il s'agit d’un dioptre sphérique caractérisé par son rayon de courbure. Une lentille sphérique est donc une succession de deux dioptres sphériques.
Une lentille sphérique est dite mince si les rayons de courbure de ses deux faces sphériques sont beaucoup plus grands que l'épaisseur de la lentille.
Il est en fait plus facile de calculer les effets d’une lentille mince que ceux d’une lentille épaisse. Pour faciliter encore le problème il est judicieux de se placer dans les conditions de Gauss, ce que nous ferons maintenant.
Lentilles divergentes et convergentes
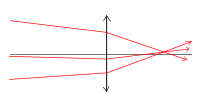
[modifier | modifier le wikicode]Selon la forme de la lentille, celle-ci peut dévier les rayons différemment. On distingue deux sortes générales de lentilles, dont les schémas sont donnés ci-dessous :
 |
 | |
| Une lentille convergente a tendance à rapprocher les rayons de l’axe optique. | Une lentille divergente a tendance à éloigner les rayons de l’axe optique. |
Centre et foyers
[modifier | modifier le wikicode]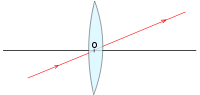
Le centre optique d’une lentille, généralement appelé O, est le point d'intersection entre le plan de la lentille et l’axe optique : un rayon passant par ce point garde la même direction.
On rappelle également la définition des foyers notés F et F' , définis dans un cours précédent :
- Le foyer objet F est le point de l’axe optique tel que tout rayon passant par F sorte parallèle à l’axe optique.
- Le foyer image F' est le point de l’axe optique tel que tout rayon passant par F ' vienne d’un rayon incident parallèle à l’axe optique.

On donne (image à gauche) un exemple du foyer objet d’une lentille convergente, où f est la distance focale, c'est-à-dire la distance entre F et O.
Relations de conjugaison et détermination d'images
[modifier | modifier le wikicode]On considère un objet AB dont l’image A'B' est formée grâce à une lentille de distance focale f, comme l'indique le schéma ci-dessous (dans le cas d’une lentille convergente et d’un objet réel).
Connaissant la distance de l’objet à la lentille, on est capable de déterminer l'endroit où va se former l’image grâce à la relation suivante.
On peut aussi se servir de la relation équivalente suivante :
Après avoir calculé la distance de la lentille à l’image, il faut savoir calculer la taille de cette image. Celle taille est reliée à la taille de l’objet par l'intermédiaire du grandissement.
Ces relations seront démontrées dans le cadre d'exercices, et il ne faut pas oublier qu’elles sont valables même si la lentille est divergente ou si l’objet est virtuel, bien que le schéma représente une lentille convergente et une image réelle.








