Initiation à l'élasticité/Principe fondamental de la statique
Introduction[modifier | modifier le wikicode]
L'objectif est de déterminer en tout point M de V.
Le principe fondamental de la statique est l'équation mécanique qui gouverne les systèmes sollicités. On cherche à écrire le PFS avec pour pouvoir utiliser les équations pour résoudre le problème.
Expression globale[modifier | modifier le wikicode]
On parle d'expression globale car l'équation concerne l’ensemble du volume considéré.

On veut le PFS pour un volume V. On fait le bilan des sollicitations:
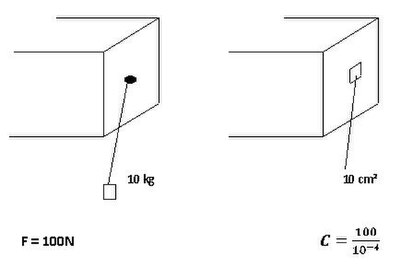
- Forces de surface: elles peuvent être exprimées par des vecteurs contraintes dont la résultante est égale aux efforts appliqués.
- Forces de volume : elles sont appliquées par unité de volume.
Exemple[modifier | modifier le wikicode]
- Forces de surface: on les traduit en contraintes en considérant la surface sur laquelle elles sont appliquées.
- Forces de volume: le poids.
Objet = 1 000 kg
masse volumique
Poids de l'objet:
Soit S' la surface de S pour laquelle on calcule les sollicitations et les vecteurs contraintes appliqués (définis par les conditions limites).
Les sollicitations extérieures sont définies par sur S' et par la force de volume exprimée par unité de volume.
On veut écrire le PFS pour V:
- Forces :
- Moments: On écrit l'équilibre des moments par rapport à 0 (origine d'un repère (O, x, y, z) orthonormé).
Soit position de M.
- Moment de :
, M point d'application de C.
On veut faire apparaitre :
On a
normal à S'
Forme globale du PFS
Cette équation est valable pour tout système mécanique statique. Cependant ce qui nous intéresse est la forme locale.
Forme locale du PFS[modifier | modifier le wikicode]
La forme locale est déterminée à partir de la forme globale, elle est utile pour les calculs en analytique.
Théorème de la divergence[modifier | modifier le wikicode]
[[[Analyse_vectorielle/Divergence#Théorème_de_la_divergence|Théorème de la divergence]]]
où est le vecteur perpendiculaire à S.
le PFS est vrai pour tout V et pour tout V' inclus dans V.
alors:
La forme locale du PFS est la suivante:
On a une symétrie de
La forme locale est un outil mathématique qui traduit l'équilibre d'un système.


















![{\displaystyle \int _{S}[{\vec {f}}+div({\tilde {\sigma }})]\mathrm {=} 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5864a957db2cad47063168c4f462efd295adf5fa)

