Approfondissement sur les suites numériques/Exercices/Ensemble de Mandelbrot

En noir, l’ensemble de Mandelbrot.

Voir aussi le TP d'informatique associé à cet exercice : Travail pratique/Fractale de Mandelbrot.

Ce problème étudie les suites complexes définies par une relation de récurrence de la forme :

$\forall n\in \mathbb {N} ,\qquad u_{n+1}=u_{n}^{2}+C$

avec C un nombre complexe fixé, le premier terme de la suite étant pris nul. La célèbre fractale de Mandelbrot est l’ensemble des points C du plan complexe tels que la suite ne diverge pas.

Les points fixes

Soit C un nombre complexe.

• Question 1 — Discuter, selon les valeurs de C, l’existence et le nombre de points fixes de la suite.
• Question 2 — Dans chacun de ces cas, étudier les intervalles stables.

Solution

Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. ^{Comment faire ?}

 

Les cycles d'ordre deux

Nous allons alors rechercher les cycles d'ordre deux, c'est-à-dire l’ensemble des points périodiques de période deux.

• Question 3 — Quelle équation doit vérifier un point z de la suite pour être périodique de période deux ? On la note (E).
• Question 4 — Montrer que les deux points fixes trouvés plus haut sont solutions de (E).
• Question 5 — On note α₁ et α₂ les deux points fixes de la partie précédente. Que valent les nombres α₁α₂ et α₁ + α₂ ?

On admet que l'équation de la question 3 peut se mettre sous la forme suivante :

$(z-\alpha _{1})(z-\alpha _{2})(z-\beta _{1})(z-\beta _{2})=0\,$

Avec β₁ et β₂ les deux autres solutions, éventuellement identiques, complexes, de l'équation.

• Question 6 — Développer et réduire cette expression. En déduire la valeur de β₁β₂ et de β₁ + β₂.
• Question 7 — De quel polynôme du second degré β₁ et β₂ sont-elles solutions ? Exprimer ces deux nombres en fonction de C.
• Question 8 — Que vaut ƒ(β₁) ? ƒ(β₂) ?
• Question 9 — Que dire alors du nombre de cycles d'ordre deux ?

Solution

Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. ^{Comment faire ?}

 

La cardioïde principale

L'ensemble des points C forme une cardioïde.

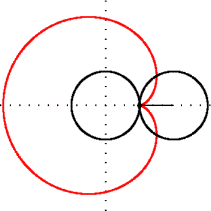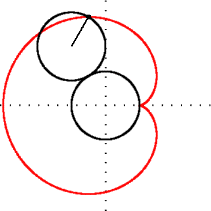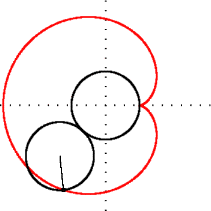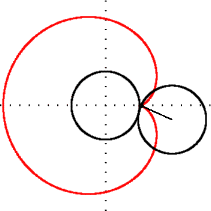
On admet que les points z vérifiant la relation :

$\left|2z\right|=1$

Sont très intéressants. Nous nous intéressons notamment dans cette partie aux points fixes z qui vérifient cette relation.

• Question 10 — En utilisant la notation trigonométrique, donner une expression de C en fonction de z.
• Question 11 — Montrer que l’on a, en coordonnées polaires, une relation de la forme : $\left|C(\theta )-1/4\right|=2r(1-\cos \theta )$. Déterminer r.
• Question 12 — Tracer l’ensemble des points C.

La figure obtenue, analogue à la courbe rouge ci-à droite, est appelée une cardioïde. Elle forme la partie visible la plus « voyante » de l’ensemble de Mandelbrot, et porte le nom de « cardioïde principale ».

Solution

Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. ^{Comment faire ?}

 

Symétrie de l’ensemble

• Question 13 — Démontrer que l’ensemble de Mandelbrot est symétrique par rapport à l’axe des abscisses.

Indication : on pourra noter M l’ensemble des points C dans l'ensemble, et montrer qu'alors (par exemple par récurrence) le nombre C*, conjugué de C, l'est également.

Solution

Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. ^{Comment faire ?}