Résistance et impédance/Impédance
Impédance
[modifier | modifier le wikicode]
Lors de mesures en courant continu, la relation entre la tension et le courant était définie par
R étant la résistance du circuit.
Pourquoi ? Car en courant continu, il n'y a que cet élément qui répond à la loi d'Ohm.
Maintenant si on passe en signal alternatif sinusoïdal, on constate que d'autres éléments, qui ne sont pas des résistances, répondent aussi à cette loi. Puisque ce ne sont pas des résistances, on ne peut pas utiliser la lettre R, ni les appeler « résistances ».
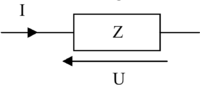
C'est pour cela qu'en alternatif, la relation s'écrit
Z étant appelée l'impédance du circuit. L'unité de Z est l'ohm [Ω] tout comme la résistance dans un circuit continu.
Cette impédance se décompose en 3 morceaux, les 3 éléments qui répondent à cette loi, appelée aussi loi d'Ohm : , et .
Rappel
[modifier | modifier le wikicode]En alternatif, la pulsation électrique ω, en radian par seconde, rad.s⁻¹, est définie par :
f étant la fréquence du signal, en hertz, Hz.
La résistance
[modifier | modifier le wikicode]Tout comme en continu, l'impédance de la résistance est égale à elle-même, quelle que soit la pulsation du courant.

Une résistance de 10 Ω en continu vaudrait 10 Ω en alternatif
L'inductance
[modifier | modifier le wikicode]En continu, l'inductance n'a pas d'effet sur un circuit, c’est tout bonnement un fil, au pire, ce n'est qu'un peu de résistance.
Par contre, elle intervient en alternatif sous la forme :

Où représente l'unité imaginaire utilisée à la place de dans ce contexte pour éviter toute confusion avec le symbole de l'intensité (en ampères).
On remarque que augmente lorsque ω augmente.
Le condensateur
[modifier | modifier le wikicode]Tout comme l'inductance, le condensateur intervient sur l'impédance du circuit :

On peut aussi remarquer que, contrairement à l'inductance, l'impédance d'un condensateur diminue lorsque ω augmente.
Exercice
[modifier | modifier le wikicode]













