Logique séquentielle/Mémoires et bascules
Mémoires RS
[modifier | modifier le wikicode]La mémoire (appelée parfois bascule monostable) est un composant permettant de retenir un bit d'information. C’est un élément qui ne peut pas être réalisé en combinatoire pur. Pour son étude il faut donc des méthodes différentes de celles du combinatoire, à savoir des tables de vérité. On utilisera cependant une table d'évolution, qui ressemble à une table de vérité.
Voir aussi bascules électroniques RS.
La description du séquentiel se fait à l'aide de deux états différents : l'état présent et l'état futur. La table qui décrit l'état futur en fonction des entrées et de l'état présent s’appelle table d'évolution (appelée aussi table de vérité ici par abus de langage).
L'état présent désigne toujours une ou plusieurs sorties de mémoire (et par la suite de bascule). L'état futur désigne ce qu’il y aura en sortie dans le futur. Le futur en question peut être très proche pour des composants modernes (inférieur à 10 ns).
Les états pour ce chapitre seront sur un seul bit. L'état présent sera noté q et l'état futur sera noté Q ou .
Voici un exemple de table d'évolution pour une mémoire RS.
- Table d'évolution
| Entrées | État futur | Fonction réalisée | |
| R | S | Q ou | |
| 0 | 0 | q | mémorisation |
| 0 | 1 | 1 | mise à un |
| 1 | 0 | 0 | mise à zéro |
| 1 | 1 | X | priorité |
Ce qui change dans cette table d'évolution par rapport à une table de vérité combinatoire, c’est la présence dans la colonne Q (ou ), de q, c'est-à-dire de l'état présent. Cela montre qu'elle exprime donc l'état futur en fonction de l'état présent q.
Toute ligne qui contient l'état présent ne peut en aucun cas être réalisée de manière combinatoire et décrit ainsi un élément séquentiel.
Cette propriété a des conséquences importantes sur les équations que l’on peut tirer d'une telle table.
L'équation obtenue à partir d'une table d'évolution est une équation de récurrence. Elle est appelée ainsi, car elle exprime Q (ou ) en fonction de q.
Je pense important de faire une mise au point avant de continuer.
La dernière ligne de la table d'évolution (pour R = S = 1) n’est pas traitée dans toute la littérature de la même manière. On trouve souvent une interdiction concernant cette ligne. Remarquez qu'alors, les sorties souhaitées sont au nombre de deux, notées Q et . En ce qui nous concerne, nous autorisons la ligne en question mais cela a un prix : on abandonne .
Revenons à notre table d'évolution donnée en exemple (ci-dessus). L'entrée S sert donc à positionner la sortie à 1, tandis que R sert à mettre à 0 (on l'appelle souvent RAZ = Remise A Zéro).
Pour éviter d'interdire la dernière ligne de la table d'évolution, nous choisissons d'étudier nos mémoires pour une seule sortie notée Q, en laissant ainsi tomber la sortie . Le X dans cette ligne représente trois cas distincts :
- X = 0, on parle de mémoire à Reset prioritaire,
- X = 1, on parle de mémoire à Set prioritaire,
- X = q, on parle alors de mémoire à mémoire prioritaire.
Une mémoire donnée ne peut que réaliser un des trois cas et son nom en découlera immédiatement.
Nous proposons le schéma suivant et son tableau de Karnaugh associé :

Nous vous proposons dans le schéma ci-dessus, deux versions de notre mémoire : un schéma croisé (à gauche) qui peut laisser penser à la présence de deux fils en forme de boucle, mais cette même mémoire en version décroisée (au centre) montre qu'une seule boucle est présente.
Remarquez la variable q introduite dans le tableau de Karnaugh (alors que le circuit n'a en réalité que deux entrées). Ce tableau de Karnaugh sert lui aussi à déduire une équation de récurrence (simplifiée dans ce cas).
L'équation de récurrence déduite exprime Q en fonction de q, R et S. Mais si vous regardez le schéma vous verrez que Q et q représentent le même fil (rouge). Il en résulte une difficulté de raisonnement, au premier abord, parce qu'un fil ne peut pas prendre deux valeurs différentes à ses deux extrémités. J'y reviens un petit peu plus tard.
L'équation de récurrence s'écrit :
Quelle est la priorité de notre mémoire donnée en exemple ?
La mémoire RS présentée ci-dessus est une mémoire à Reset prioritaire car la colonne pour R=1 et S=1 nous montre deux 0. Quand la mise à un (S) et la mise à zéro (R) "se battent", c’est le R qui gagne.
Je vous avais promis de revenir sur la difficulté de raisonnement liée au fait que notre fil rouge avait deux valeurs éventuellement différentes à ses extrémités.
Prenez l'habitude de raisonner sur un schéma décroisé. Sur ce schéma vous imaginez un axe des temps allant de la gauche vers la droite. Ce n’est pas si stupide que cela car vos portes logiques mettent un certain temps pour "calculer" leurs sorties. Du coup, si à gauche vous avez l'état présent "q", vous aurez à droite l'état futur "Q" qui sera fonction de q, R et S.
Exercice 1
[modifier | modifier le wikicode]Pour le schéma ci-dessous, compléter le tableau de Karnaugh ainsi que le diagramme des temps. On supposera pour simplifier que les portes répondent de manière instantanée (ce que l’on a toujours fait jusqu'à maintenant).

Vous pouvez vous faire une idée de la table de vérité en consultant le cours sur les bascules en portes NAND. Notez-y que la table de vérité présentée interdit la première ligne alors que moi je l'autorise. Voici donc ma version de la table d'évolution :
Sur cette table, les deux sorties sont et . Remarquez que l'état présent est noté et l'état futur ce qui est une notation très souvent utilisée.
Pour R=1 et S=1, ces deux sorties ne sont pas le complément l'une de l'autre (dernière ligne). Pour éviter ce genre de conflit, soit on n'autorise pas la ligne, soit on étudie une seule sortie, soit on étudie les deux sorties en admettant qu’elles ne sont pas toujours complémentaires. Dans ce document on n'adoptera jamais la première solution.
La mémoire RS présentée ci-dessus est une mémoire à Set prioritaire car la ligne pour R = 1 (/R = 0) et S = 1 (/S = 0) nous montre deux 1. Quand la mise à un (Set) et la mise à zéro (Reset) "se battent", c’est le Set qui gagne sur .
Mémoire D (D latch)
[modifier | modifier le wikicode]Cette fonction comporte deux entrées D et H et une sortie Q. L'équation de récurrence de la mémoire D n'a pas beaucoup d'intérêt, il vaut mieux retenir son fonctionnement : recopie son entrée D sur sa sortie Q lorsque son horloge H est à 1.
Bascules électroniques D
[modifier | modifier le wikicode]On appelle front d'horloge tout changement d'horloge. Ainsi le passage d'une horloge de la valeur '0' à la valeur '1' sera nommé front montant et le passage d'une horloge de la valeur '1' à la valeur '0' sera nommé front descendant. On parle aussi parfois de flanc montant et de flanc descendant.
Cette bascule comporte aussi deux entrées, D et H et une sortie Q, comme la mémoire D. La grande différence est que la recopie de l'entrée sur la sortie ne se fait maintenant que sur flanc montant de l'horloge. Notez sur le schéma ci-dessous comment est notée cette sensibilité au flanc montant de l'horloge.
La bascule D la plus complexe comporte quatre entrées D, H, S et R et une sortie Q. Les entrées supplémentaires sont actives à l'état bas (donc notées parfois /S et /R) et ont les mêmes fonctions que dans le cas d'une mémoire. Elles sont dites asynchrones dans le sens où contrairement à D elles sont complètement indépendantes des flancs montants de l'horloge.
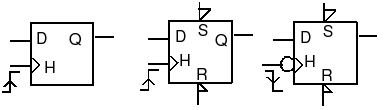
Plus d'information ici : Bascules électroniques.
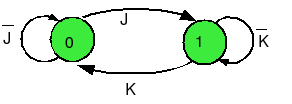
Bascules électroniques JK
[modifier | modifier le wikicode]D'autres informations ici : la bascule JK.
Nous complétons cette information par ce que l’on appellera, dans la suite de ce cours, un diagramme d'évolution. Ici, il est constitué de deux états (en vert) et de transitions (les flèches). Ce diagramme d'évolution est très important pour nous car il nous servira lors de nos synthèses. Il remplace la table de vérité de la bascule JK.
Voici aussi sous forme de diagramme temporel le fonctionnement d'une JK.
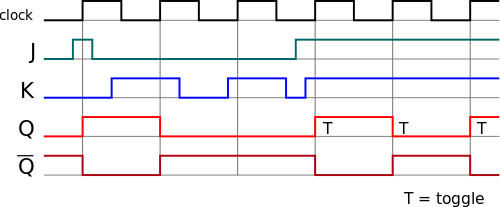
Le "T = Toggle" qui est présent dans la figure se traduirait par "B = Basculement" en français.
Exercice 2
[modifier | modifier le wikicode]Transformer une bascule JK en bascule D. Transformer ensuite une bascule D en bascule JK.
Exercice 3
[modifier | modifier le wikicode]Nous désirons réaliser la bascule E suivante.
- si E=0 alors Q=0
- si E=1 alors Q(n+1) = /Q(n).











