Dynamique des fluides parfaits/Exercices/Véhicule à coussin d'air
On veut construire un véhicule à coussin d'air de forme circulaire et de rayon R. Le rotor aspire l'air ambiant et le comprime à la pression P0 supposée uniforme sous le carter. À l'équilibre le débit aspiré par le rotor est égal à celui qui s'échappe sous la jupe du véhicule située à une hauteur h au-dessus du sol, et le poids W du véhicule est supporté par la pression régnant sous le carter.
1. Montrer que la vitesse de l’air sous le carter est négligeable devant la vitesse de l’air qui s’échappe sous la jupe et calculer le débit Q aspiré par le rotor en fonction de W, R, h, de la pression atmosphérique et de la masse volumique de l’air.
2. La puissance fournie par le rotor étant de P et le rendement du rotor étant de 0,7, calculer la garde au sol h.
3. Étudier la stabilité verticale du véhicule : comment évolue les forces de pression si h change pour Q constant ?
Données pour l'analyse numérique :
- AN : W = 12 000 N
- R = 1,5 m
- P = 50 kW
1. On néglige toutes les pertes de charge dues à l'écoulement, on a alors l'équilibre :
L'équation de Bernouilli donne, entre 0 et 2 :
Avec la convention suivante :
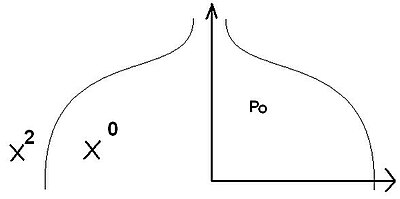
On suppose que
Et on a alors :
La conservation du débit donne alors :
On a alors :
On a finalement :
2. Si on néglige les effets visqueux, on a , avec la puissance utile.
On a
On a donc :
Avec
On a donc :
En application numérique, on trouve :
3. On a , avec force de pression, et car .
Si h augmente, alors diminue, et donc h diminue, et inversement. On en conclue qu’il y a stabilité du système.






















