En raison de limitations techniques, la typographie souhaitable du titre, «
Exercice : Théorème de ThalèsTriangles et parallèles/Exercices/Théorème de Thalès », n'a pu être restituée correctement ci-dessus.
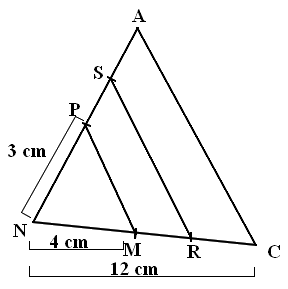
NAC est un triangle. On suppose que :
(PM) est parallèle à (AC) ; (RS) est parallèle à PM ;
P appartient à [AN]; M appartient à [CN]; R appartient à [MC]; S appartient à [PA] ;
NM = 4 cm cm cm Schéma 1. Écrire toutes les égalités qui résultent de la propriété des 3 rapport égaux en précisant le triangle concerné.
2. Calculer la longueur PA.
Solution
1. Dans le triangle NRS :
N
P
N
R
=
N
M
N
C
=
P
M
R
S
{\displaystyle {\frac {NP}{NR}}={\frac {NM}{NC}}={\frac {PM}{RS}}}
Dans le triangle NAC :
N
P
N
A
=
N
M
N
C
=
P
M
A
C
{\displaystyle {\frac {NP}{NA}}={\frac {NM}{NC}}={\frac {PM}{AC}}}
N
R
N
A
=
N
S
N
C
=
R
S
A
C
{\displaystyle {\frac {NR}{NA}}={\frac {NS}{NC}}={\frac {RS}{AC}}}
2. Dans le triangle AMC, on a :
N
P
N
A
=
N
M
N
C
=
P
M
A
C
{\displaystyle {\frac {NP}{NA}}={\frac {NM}{NC}}={\frac {PM}{AC}}}
Produit en croix de
3
x
=
12
4
{\displaystyle {\frac {3}{x}}={\frac {12}{4}}}
Or
N
A
=
9
{\displaystyle NA=9}
P
A
=
x
−
3
=
9
−
3
=
6
c
m
{\displaystyle PA=x-3=9-3=6cm}
P
A
=
6
c
m
{\displaystyle PA=6cm}
Démonstration : À un tiers de sa hauteur, une pyramide occupe deux tiers de son volume total [ modifier | modifier le wikicode ] Le volume d'une pyramide de hauteur
H
{\displaystyle H}
L
{\displaystyle L}
H
L
2
3
{\displaystyle {\frac {HL^{2}}{3}}}
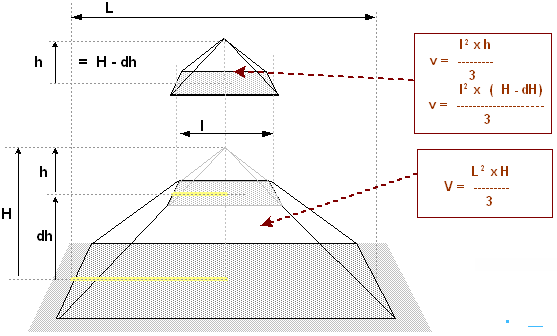
L'évolution du volume de la pyramide revient à tronquer celle-ci par une plus petite partant du sommet [ modifier | modifier le wikicode ] Partons du schéma ci-dessous
Dans le schéma, le volume de la grande pyramide vaut
V
=
H
L
2
3
{\displaystyle V={\frac {HL^{2}}{3}}}
v
=
h
l
2
3
{\displaystyle v={\frac {hl^{2}}{3}}}
La hauteur de la pyramide tronquée peut s'obtenir à partir des hauteurs des deux pyramides par la formule :
d
h
=
H
−
h
{\displaystyle \mathrm {d} h=H-h}
On peut alors exprimer le pourcentage d’évolution de la pyramide par :
∂
h
=
d
h
H
{\displaystyle \partial h={\frac {\mathrm {d} h}{H}}}
Du coup
h
=
H
−
d
h
=
H
−
H
∗
∂
h
=
H
(
1
−
∂
h
)
.
{\displaystyle h=H-\mathrm {d} h=H-H*\partial h=H(1-\partial h).}
Si on fait varier la hauteur de la petite pyramide de cette manière
h
:
H
↘
0
{\displaystyle h:H\searrow 0}
d
h
{\displaystyle \mathrm {d} h}
0
↗
H
{\displaystyle 0\nearrow H}
∂
h
{\displaystyle \partial h}
0
↗
100
%
{\displaystyle 0\nearrow 100\%}
On peut appliquer le théorème de Thalès dans le schéma et relier les dimensions des deux pyramides. On obtient :
h
H
=
l
2
L
2
=
l
L
{\displaystyle {\frac {h}{H}}={\frac {\frac {l}{2}}{\frac {L}{2}}}={\frac {l}{L}}}
Donc on peut exprimer
l
{\displaystyle l}
L
{\displaystyle L}
∂
h
{\displaystyle \partial h}
l
=
L
∗
h
H
{\displaystyle l=L*{\frac {h}{H}}}
l
=
L
∗
H
∗
(
1
−
∂
h
)
H
=
L
∗
(
1
−
∂
h
)
{\displaystyle l=L*{\frac {H*(1-\partial h)}{H}}=L*(1-\partial h)}
Le remplissage de la pyramide tronquée est donc
V
T
=
V
−
v
=
V
−
h
∗
l
2
3
{\displaystyle VT=V-v=V-{\frac {h*l^{2}}{3}}}
Ce qui donne
V
T
=
V
−
(
H
(
1
−
∂
h
)
)
∗
(
L
(
1
−
∂
h
)
)
2
3
=
V
−
V
∗
(
1
−
∂
h
)
∗
(
1
−
∂
h
)
2
{\displaystyle VT=V-{\frac {(H(1-\partial h))*(L(1-\partial h))^{2}}{3}}=V-V*(1-\partial h)*(1-\partial h)^{2}}
Soit encore
V
T
=
V
∗
(
1
−
(
1
−
∂
h
)
3
)
=
V
∗
(
1
−
(
1
−
3
∂
h
+
3
∂
h
2
−
∂
h
3
)
)
=
V
∗
(
3
∂
h
−
3
∂
h
2
+
∂
h
3
)
{\displaystyle VT=V*(1-(1-\partial h)^{3})=V*(1-(1-3\partial h+3\partial h^{2}-\partial h^{3}))=V*(3\partial h-3\partial h^{2}+\partial h^{3})}
L’évolution du remplissage de la pyramide tronquée est égal à
∂
V
T
=
V
T
V
=
3
∂
h
−
3
∂
h
2
+
∂
h
3
{\displaystyle \partial VT={\frac {VT}{V}}=3\partial h-3\partial h^{2}+\partial h^{3}}
À un tiers de sa hauteur, le volume rempli de la pyramide est donc de :
3
∗
1
3
−
3
(
1
3
)
2
+
(
1
3
)
3
=
∂
V
T
1
/
3
=
1
−
1
3
+
1
27
=
2
3
+
1
27
{\displaystyle 3*{\frac {1}{3}}-3({\frac {1}{3}})^{2}+({\frac {1}{3}})^{3}=\partial VT1/3=1-{\frac {1}{3}}+{\frac {1}{27}}={\frac {2}{3}}+{\frac {1}{27}}}
2
3
{\displaystyle {\frac {2}{3}}}
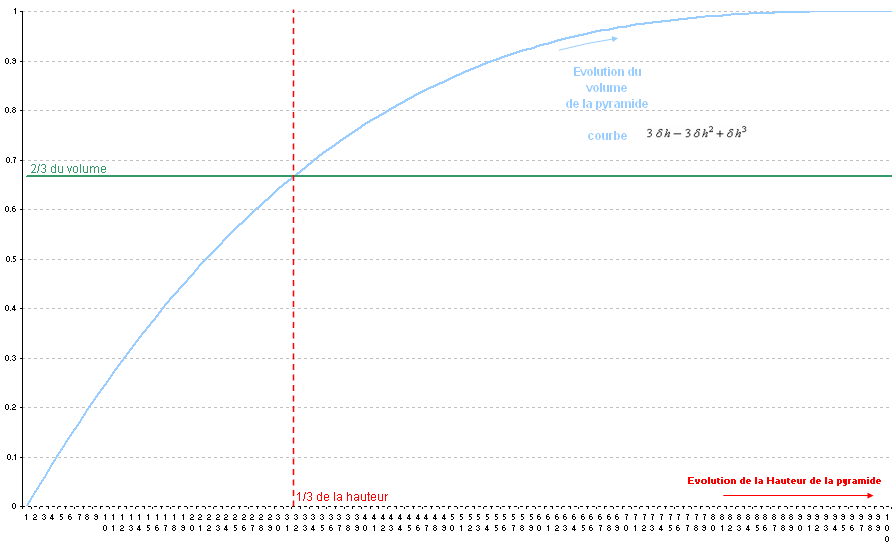
Si on trace la courbe
3
∂
h
−
3
∂
h
2
+
∂
h
3
{\displaystyle 3\partial h-3\partial h^{2}+\partial h^{3}}